一百多年前，人们发现在特殊体系做电磁测量时，电场能够产生磁化的同时磁场能产生电极化，这种现象被称为磁电耦合。2008年，斯坦福大学祁晓亮等人提出了拓扑磁电耦合，相应体系中可观测到半整数量子化的霍尔效应（Physical review B 78, 195424，2008）。随后，在具有磁电耦合的拓扑体系中，发现了许多新奇效应，例如负磁阻效应、手征磁效应、磁光效应等。

磁电耦合可以通过P = αB，M = αE来描述，其中P是电极化强度，B是磁场，M是磁化强度，E是电场，α是磁电耦合系数。进一步，我们可以得到极化电流j_p与束缚电流j_b：

j_p = ∂_t P = ( ∂_t α )B + α( ∂_t B )

j_b = ∇ × M = ( ∇ × α ) ⋅ E + α( ∇ × E )

以及总的电流响应：

j = j_p + j_b = ( ∂_t α )B + ( ∇ × α ) ⋅ E

其中有两项由于法拉第电磁感应定律 ∂_t B = -∇ × E相互抵消，剩下的第一项被称为动力学轴子响应（Nature Physics 6, 284, 2010），而第二项便是拓扑磁电耦合体系中半整数量子化的霍尔效应的来源。

最近，williamhill体育入口注册量子材料科学中心博士后王茂原，在合作导师谢心澄院士的指导下，与北京师范大学物理学系刘海文教授合作，深入研究了新型反对称磁电耦合，相应体系能够实现由含时变化磁场驱动产生同方向电流响应j^β = 2β∂_t B。具体来说，相比之前提到对称的磁电耦合α反对称磁电耦合β的反对称性体现在：

P = (α + β) B

M = (α – β) E

即在电场产生磁化与磁场产生电极化的相应系数互为相反数。同时，反对称磁电耦合β依赖于电磁场频率ω，一般写作β(ω)。有了反对称磁电耦合β(ω)之后，代入之前电流响应，可以得到

j = j_p + j_b = ∂_t [ α + β(ω) ]B + { ∇ × [ α - β(ω) ] } ⋅ E + 2β(ω)∂_t B

这里便产生了含时变化磁场驱动产生同方向电流响应j^β = 2β(ω)∂_t B。

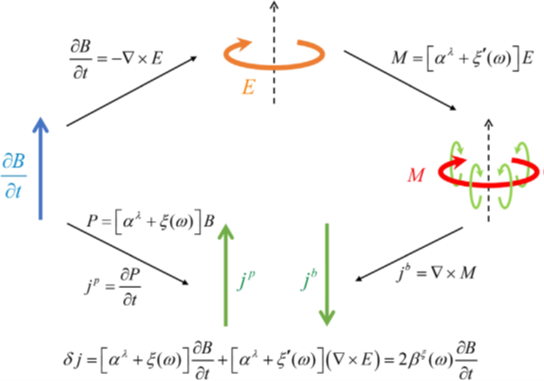
图 反对称磁电耦合的示意图

图中包括 (1) 极化电流j_p = ∂_t P，P为磁电耦合诱导的电极化强度; (2)法拉第定律∂_t B = -∇ × E; (3)磁电耦合诱导的磁化强度M; (4) 束缚电流j_b = ∇ × M。考虑新型反对称磁电耦合后，时变磁场会诱导出动态磁电流δj = 2β^ξ(ω)∂_t B，β^ξ(ω) = [ ξ(ω) - ξ’(ω)] / 2。

对称的磁电耦合α与反对称的磁电耦合β(ω)的物理来源有所不同。对称的磁电耦合α体现了磁电耦合中电场E与磁场B的对易性，而反对称的磁电耦合β(ω)则是体现了电场E与磁场B的反对易性，而这来源于量子力学的中的推迟响应（retarded response），可以用Kubo公式进行描述。根据对称性分析研究，具有反对称磁电耦合的体系需要破缺时间反演、空间反演以及镜面反演对称性。因此，团队挑选了反铁磁体系Mn₂Bi₂Te₅作为候选材料，研究了自旋轨道耦合强度以及电磁场频率ω对反对称磁电耦合大小的影响，并简单设计了实验观测方案。

2022年6月10日，相关研究成果以“新型含时反对称磁电耦合”（New Type of Anticommutative Dynamical Magnetoelectric Response）为题在线发表于《物理评论快报》（Physical Review Letters）。王茂原为第一作者与通讯作者，刘海文和谢心澄为共同作者。

上述研究工作得到国家重点研发计划、国家自然科学基金、中国科学院战略性先导科技专项、中国博士后科学基金等的大力支持。

论文链接：https://journals.aps.org/prl/abstract/10.1103/PhysRevLett.128.236601