williamhill体育入口注册凝聚态物理与材料物理研究所赵宏政助理教授与合作者在数字化量子动力学模拟领域取得重要进展。研究团队将自适应步长的演化算法拓展至随时间变化的多体哈密顿量动力学模拟。2024年7月3日，相关成果以“利用分段守恒定律的含时哈密顿量动力学的自适应Trotter算法”（Adaptive Trotterization for time-dependent Hamiltonian quantum dynamics using piecewise conservation law）为题，在线发表于《物理评论快报》（Physical Review Letters） 上。

量子多体系统的非平衡动力学演化是十分丰富且极为复杂的，对于它们的研究，解析求解或者利用经典计算机直接进行数值模拟的方法通常非常有局限性，很难给出令人满意的描述。近年来，量子模拟平台在空间和时间上的操控水平突飞猛进，这使得我们利用它们来模拟复杂的量子多体动力学成为可能。

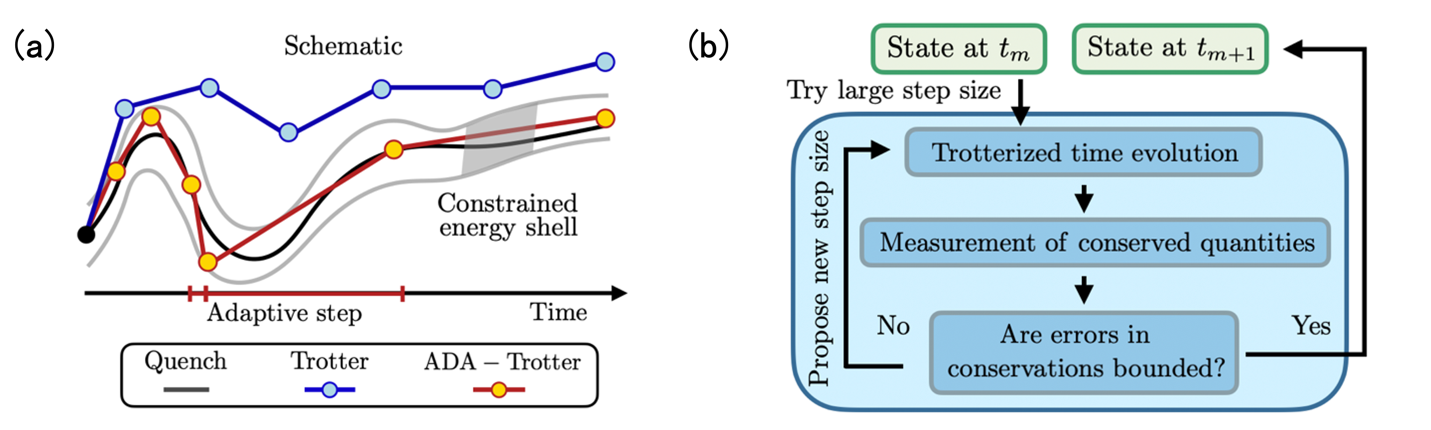
图1：（a）演化示意图，ADA-Trotter能够将量子态的演化严格限定在正确的能量壳层上，固定步长的算法则不然ADA-Trotter算法。（b）利用反馈调节自适应改变演化步长。

数字化量子模拟（Digital quantum simulation）是其中一种可能的方法，其基本思想是将连续时间演化算符离散为基本的少体量子门，即所谓的Trotterization过程。然而，由于这些量子门的非对易性，Trotterization会引入计算误差，在较长的模拟时间内会逐渐积累。尽管使用较小的演化步长可以提高模拟精度，但也会相应增加电路深度。在当前含噪声的量子模拟平台上，量子门的缺陷是不可避免的，这对提高量子模拟的准确性构成了重大挑战。因此，探索能够保持模拟精度的同时又能最小化电路深度的算法对于量子模拟来说意义重大。

在之前的工作中，研究团队受到了自适应步长的经典算法的启发（例如Runge–Kutta方法），提出了一种自适应步长的量子算法，ADA-Trotter【PRX Quantum 4, 030319(2023)】。此算法使用测量的手段来监控不含时间的哈密顿量系统的能量及其涨落的误差（图1a），利用中心极限定理的原理，通过一个反馈的过程来自适应地调节时间演化步长（图1b）。这种反馈过程不仅使得量子动力学模拟的计算资源被更加高效利用，还可以将量子态限定在正确的能量壳层中，避免能量误差的累积。

然而，将这种算法扩展到时间依赖的哈密顿量是一个十分具有挑战性的问题。因为系统本身不再能量守恒，很难定义改变演化步长的判断标准。本文中，研究团队提出新的tADA-Trotter的算法来针对性地解决这个问题。此算法的核心是首先将哈密顿量在时间上的变化离散化，并通过微扰论的手段来解析推导出系统中存在的分段守恒定律（图2a）。随后，利用此守恒定律的均值和方差作为标准，自适应调整演化步长，显著提升量子模拟的精确度（图2b）。

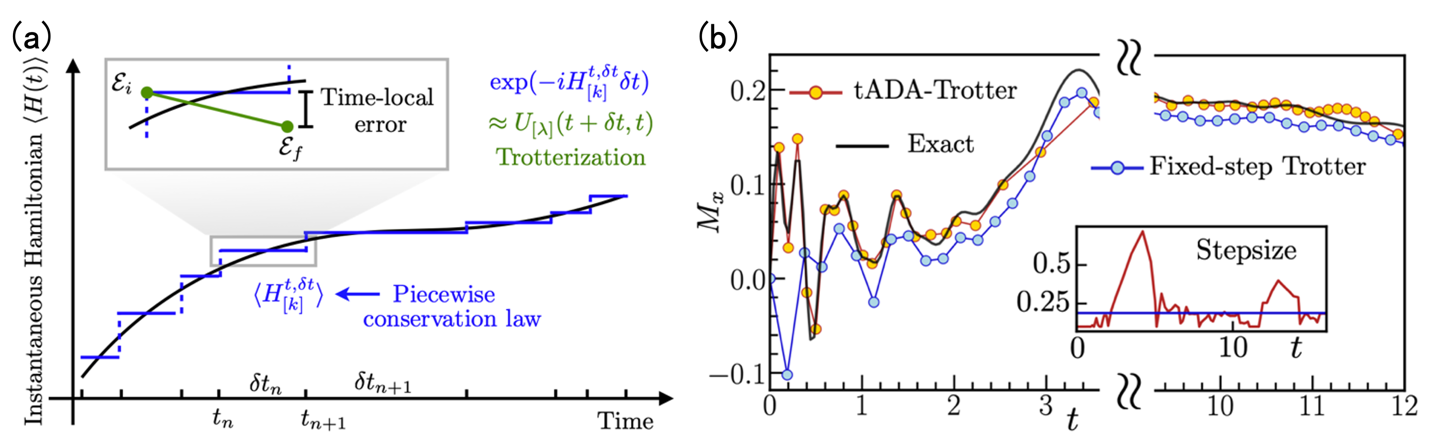
图2：（a）tADA-Trotter的示意图。将哈密顿量的时间变化离散化，利用分段守恒定律调整Trotter演化步长。（b）自适应算法与固定步长算法的对比。

赵宏政为论文第一作者及通讯作者，其他合作者包括德国马克斯-普朗克复杂系统物理研究所的Marin Bukov研究员、Roderich Moessner教授，以及德国奥格斯堡大学的Markus Heyl教授。研究工作得到了国家自然科学基金以及williamhill威廉希尔官网基本科研业务费支持。

论文原文链接：https://link.aps.org/doi/10.1103/PhysRevLett.133.010603